有损传输线模型

1 有损传输线的建模

在理想传输线中只需考虑电容和电感，但在实际传输线中存在能量的损耗，需要引入:

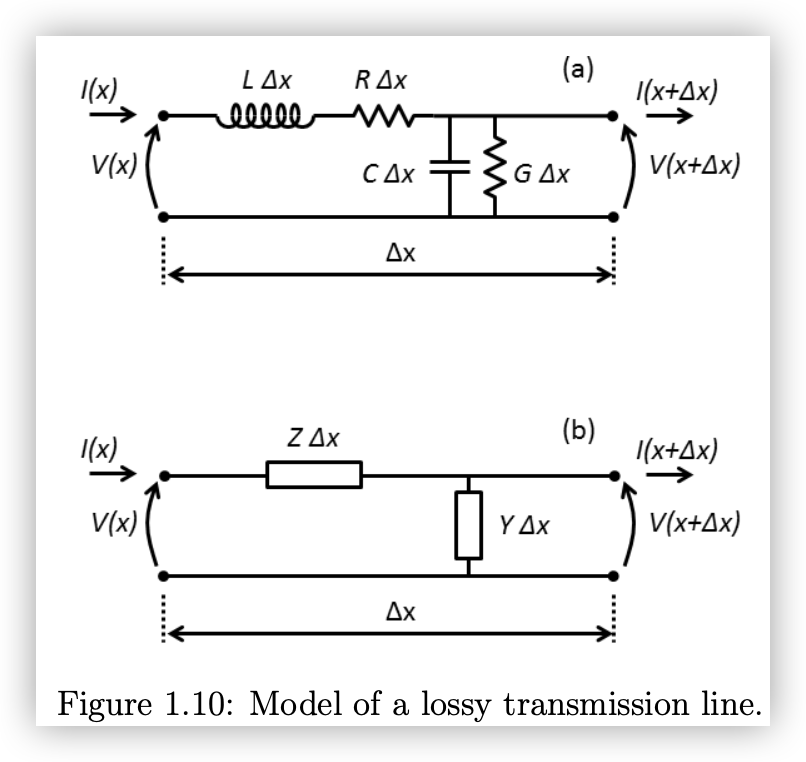
图中第一张为分布参数模型，包含以下参数:

图中第二张为简化模型，将串联的电阻与电感合并，并联的电导与电容合并:

我们只讨论正向传播的正弦波:

V (x, t) = V_{+} e^{- i k x} e^{i w t}

I (x, t) = I_{+} e^{- i k x} e^{i w t}

在时域里，根据电报方程telegrapher equation，在有电阻电导的情况下:

\frac{\partial V (x, t)}{\partial x} = - L \frac{\partial I}{\partial t} - R I

\frac{\partial I (x, t)}{\partial x} = - C \frac{\partial V}{\partial t} - G V

而我们考虑的是单一频率的正弦波，可以转换成频域形式:

\begin{matrix} (1) & i k V_{+} = Z (w) I_{+} \end{matrix}

\begin{matrix} (2) & i k I_{+} = Y (w) V_{+} \end{matrix}

如何从时域转换成频域

相量表示： 设时域信号为

V (x, t) = V_{+} e^{- i k x} e^{i w t}

I (x, t) = I_{+} e^{- i k x} e^{i w t}

时间导数替换： 因为

\frac{\partial}{\partial t} (e^{i ω t}) = i ω e^{i ω t},

所以在频域中采用

\frac{\partial}{\partial t} ⟶ i ω .

代入并应用替换得到频域电报方程：

\frac{d V (x, t)}{d x} = - (R + i ω L) I (x) \equiv - Z (ω) I (x),

\frac{d I (x, t)}{d x} = - (G + i ω C) V (x) \equiv - Y (ω) V (x),

其中

Z (ω) = R + i ω L, Y (ω) = G + i ω C .

而

\frac{d V (x, t)}{d x} = - i k V_{+} e^{- i k x} e^{i w t} = - i k V_{+}

同理可得

\frac{d I (x, t)}{d x} = - i k I_{+} e^{- i k x} e^{i w t} = - i k I_{+}

代入上式:

\frac{d V (x, t)}{d x} = - (R + i ω L) I (x) \equiv - Z (ω) I (x),

\frac{d I (x, t)}{d x} = - (G + i ω C) V (x) \equiv - Y (ω) V (x),

消去两边负号可得频域中信号的表达式:

i k V_{+} = Z (w) I_{+}

i k I_{+} = Y (w) V_{+}

将公式 1 和公式 2 相乘可得:

i^{2} k^{2} V_{+} I_{+} = Z (w) Y (w) V_{+} I_{+}

整理可得

k = \sqrt{- Z (w) Y (w)}

将公式 1 和公式 2 相除可得:

\frac{V_{+}}{I_{+}} = \frac{Z (w) I_{+}}{Y (w) V_{+}}

两边同时乘 $\frac{V_{+}}{I_{+}}$ 并开根号可得特性阻抗 $Z_{0}$ :

Z_{0} = \frac{V_{+}}{I_{+}} = \sqrt{\frac{Z (w)}{Y (w)}}

在有损传输线中， $Z (w)$ 取决于串联的每单位长度的 $L$ 和 $R$ :

Z (w) = i w L + R

同时 $Y (w)$ 取决于并联的每单位长度的 $C$ 和 $G$ :

Y (w) = i x C + G

代入可得相量常数:

k = \sqrt{- (i w L + R) (i w C + G)} = w \sqrt{L C} \sqrt{1 - i (\frac{R}{w L} + \frac{G}{w c}) - \frac{R G}{w^{2} L C}}

在低损耗的传输线中:

R ≪ w L, G ≪ w C

可以根据 $\sqrt{1 + x} ≃ 1 + x / 2 (| x | ≪ 1)$ 来展开平方根来估算 k 值:

k ≃ w \sqrt{L C} - \frac{i}{2} (R \sqrt{\frac{C}{L}} + G \sqrt{\frac{L}{C}})

现在 k 既有实数部分也有虚数部分。为进一步观察其虚数部分的影响，可写出波的空间部分:

e^{- i k x} = e^{i β x} e^{- a x}

其中

β = - w \sqrt{L C}

α = - \frac{1}{2} (R \sqrt{C} L + G \sqrt{L} C)

在有损传输线中传播的波以指数级衰减。